2013.09.27 心理及教育統計(二)

描述統計(資料展示)

note：IRS編碼為67

note2：提問的方式以及提供之資訊，可影響思考與回答之方向。

Review

• 描述統計 Vs 推論統計：
• 描述統計為對統計結果之解釋，給予其意義與結論，可使用表、圖、數值呈現。
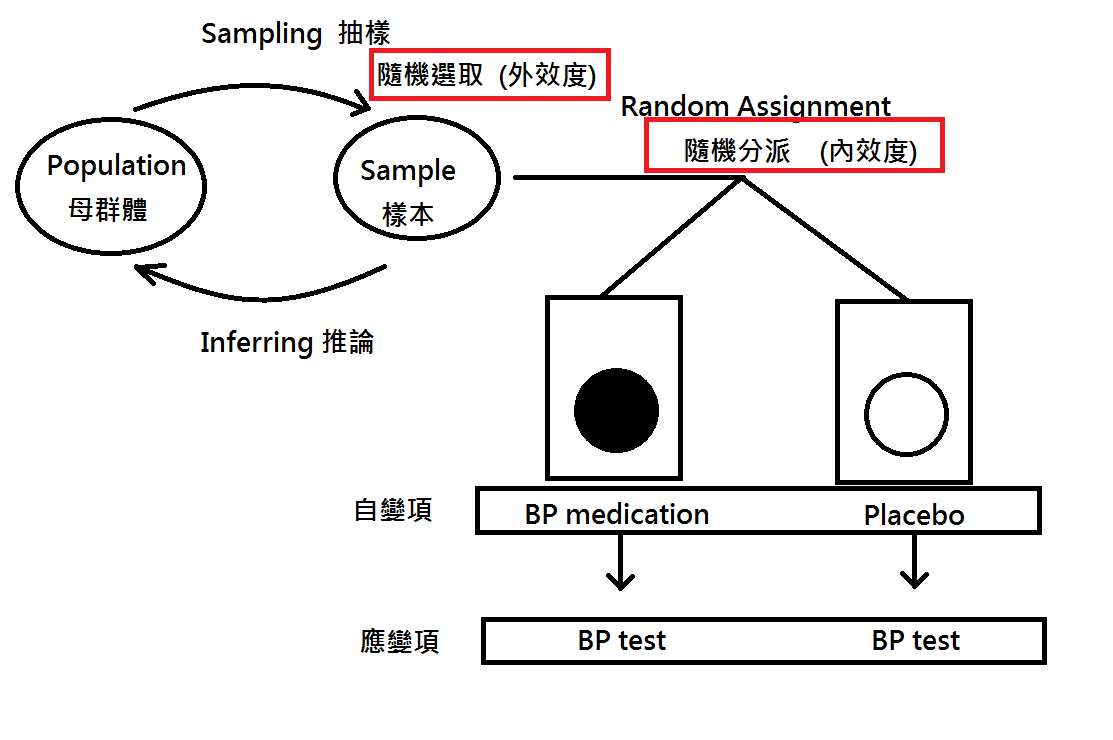
• 推論統計可分為母群體以及樣本，透過樣本推論母群體之樣貌，其隨機抽樣狀況好則代表樣本具代表性，因而其外效度佳。
• 取樣方式有四：方法可以合併使用，以提升效能。
1. 簡易取樣
2. 分層取樣
3. 系統取樣
4. 聚落取樣：較具經濟效益。
• 符號應用：母群體以希臘文為主，樣本以英文符號為主。
• 隨機取樣vs隨機分派：
• 隨機取樣越好，樣本代表性越佳，則其外效度越佳。
• 隨機分派為抽取樣本之後，於實驗中分組之程序，若分派得宜則其內效度較佳。
  
• 變項：
• 連續變項：為範圍之概念，一個數值其實包含上下一段區間，如5.0代表4.5~5.4之間。
• 間斷變項：數值間不可再細分之項目，如跳繩的次數。
• Stevens之分類共有四項：
• 名義變項：用以區辨個體之編號，本身不具大小優劣意義，也不可以計算。
• 次序變項：可區辨個體，並且數值可區辨優劣，然不具等距特質，因而不可計算。
• 等距變項：數值差異具有等距意涵，可進行數值比較與計算之功能。
• 比率變項：存在絕對零作為基準，數值間的差異存有比率上的意義。
• 質Vs量
• 母數Vs無母數：
• 有母數統計：假設常態分佈，多用於等距/比率變項，使用估計值推論母群參數。
• 無母數統計：無須假設常態分佈，多用於名義/次序變項，不需使用估計值與參數。

描述統計：資料展示

描述統計，常用表、圖、數值等方式，呈現資料。

• 表：將頻率與次數製成表格，陳列數字與相關資料，常見項目有頻率(次數)、累計次數、累計百分比等，如次數分配表(frequency distribution)。
• 分組：
• 全距(range)：最高、最低分數之差距。
• 組距：全距除以期望分組數(常為10~15)
• 以四捨五入計算之。
• 連續變項，其具有範圍性，且最低標準納入該組內，如44.5納入45-49組別，而49.5則納入50-54組別。
  note：群組左半邊的數值，應能組距所整除。
• 圖：直條圖、折線圖、圓餅圖...etc。
• 直方圖(histogram)：以直條方式描述項目與頻率，若為連續變項，則圖形將連續緊靠；如非連續變項，則彼此分離
• 折線圖、多邊圖(polygon)：將各直方圖中間點之最高點連接起來，雙邊收尾方式依學派而分。
• 圓形比例圖(pie chart)
• 莖葉圖(stem-and-leaf)：莖為主幹(此指分數十位數)，葉為個體(此指分數個位數)，優點有四：一、資料大致分配情形。二、個資料細部資訊。三、有無界外值。四、資料之偏態情形。(但粗略之莖葉圖，其特質未必優於長條圖)。
• 莖可使用組距方式，葉可計算個體以及實際數字表示。
• 界外值(outliers)：超過兩個組距以上之分數落點。
• 資料分配之形狀
• 常態(normal)
• 正偏(positively skewed)：偏，代表極端數值之所在，正偏代表極端數值在較大處。
• 負偏(negatively skewed)：負偏代表極端數值在較小處。
  P.s)事實上正偏、負偏之判讀，有其數值上之計算，然若於無工具且僅有圖形時，則以目測粗估之。
• 矩形(uniform)
• 高狹(leptokurtic)：此以厚(thick)薄 (thin)描述其兩邊之數量大小，如曲線下面積相等，則兩邊人數少則中間人數必然多。高狹則表示兩側人數少，而中間特別多之狀況。
• 低闊(platykurtic)：兩邊人數多，因而中間人數相對多(但沒有明顯超過)之狀況。
• 雙峰(bimodal)
• U形(U-shaped)
• J形(J-shaped)
• 資料分配之性質：
• 集中情況：分數集中在何處？換言之，大部分的分數落在哪個區域？
• 分散情況：分數離平均數之遠近。
• 偏態：分數分布傾向程度。
• 峰度：尾巴之厚(thick)薄(thin)，所謂厚薄可視為兩端人數之多寡，因總人數(曲線下面積)相同，因而若兩側人數少中間必然高(反之亦然)。

描述統計：集中趨勢指標與離散趨勢指標

描述統計，可以表、圖、數值方式描述之，於圖的描述，可檢視其偏鋒，而從數值描述，則檢視其集中趨勢與離散趨勢。

集中趨勢指標：從眾多數值中，找出可代表此資料之數值。

• 眾數(mode,Mo)：資料中最多數量之數值。
• 優點：
1. 可實質觀察到，此分數確實存在(而非計算出之虛值)，
2. 可代表大多數。
3. 唯一可用於名義資料 (nominal data)，而中數與平均數皆無法應用，前者因數值無順序意義，後者則為名義資料無法計算。
4. 不受極端值影響。
• 缺點：
1. 受如何分組影響。
2. 可能無法代表全體。
3. 不能用於推論統計。
• 中數(median,Mdn)：最中間之數值。
• 優點：
1. 不受極端值影響，相較於平均數，更適合描述偏態資料之集中趨勢，因此若資料有偏態時，建議使用中數計算之。
2. 對順序資料(ordinal data)特別有效，換言之將原始分數轉換經過順序排列後，即便於操作，亦可用於等距以及比例資料。
3. 可用於open-ended categories(將資料簡化，知道詳細數值而歸類於大高族群，如5↑)以及undeterminable score(簡化資料，但不知實際值，而歸類其中)。
4. 計算中數不需對等距分數有任何假設，相對於平均數而言(假設單位等距，因而可計算之)。
• 缺點：
1. 此數值可能不實際存在，特別發生於數目為偶數時。
2. 不可在equation(絕對值)中使用此值運算，因其近似於基本定義。
3. 不穩定，且隨樣本改變，如中數相同但樣本不相似，或者中數不同，但其樣本相似。
4. 操作：各分數之總數目可能為基數或者偶數時...
• 當數目為奇數：最中間的數字，第(N+1)/2個數值。
• 當數目為偶數：最中間兩個數字之平均，為N/2+(N/2+1)之平均。
• 平均數(mean,X-bar)：算術平均數(牽扯計算，需具備等距特質)。
• 優點：
1. 容易計算，最常使用。
2. 是估計母群體平均值的良好指標。
3. 使用所有數據資料。
4. 適用於等距與比例資料，但不可用於順序資料(ordinal data)，因其不具計算性。
5. 可用於計算，用於統計推論、假設檢定。
6. 較穩定，不會隨樣本而變，樣本平均數是估計母群體平均數好的估計值。
7. 求取變異數與標準差值，較偏好使用平均值而非中位數，因對於距離處理的部分較符合統計之理念(避免使用絕對值，需判斷正負，但仍可表達距離)。
• 缺點：
1. 易受極端值影響。
2. 可能實際不存在。
3. 不適用於open-ended categories 或undeterminable scores。
4. 計算分數時，需有等距之假設(152cm至153cm之1cm差距，等同187cm與188cm之1cm差距)。
   P.s) 兩個minimize的故事：
• Sum of |X-C|之最小值，C為Mdn。
• Sum of (X-C)^2之最小值，C為Mean。
  note：mean的概念是讓左右兩側的力矩(頻率*距離)相等，上述計算可簡化為2*f*D^2(D為距離、f為頻率)，因距離以二次方成長，因此控制D將使之最小；反之，Mdn的概念則次序中取中間的數值，上述計算可簡化為D*f(同上)，就方向性而言D是遞增(小至大)/遞減(大至小)的，而f提升的時候，會延緩D改變的速率，因此達成平衡的結果。
• 變化特質：
• 全體±C，則平均數則±C。
• 全體放大C倍，則平均數放大C倍。
• 所有的標準差之總和為0。
• 最小的距離平方差，必為平均數(least square property,最小平方特質)

• 長相關係：
• 當分布為對稱時：平均數=中數。
• 當分布對稱且單峰：平均數=眾數=中數。
• 當分布為正偏時：眾數(最高處)<中數(左右平均分布處)<平均數。
• 當分布為負偏時：眾數>中數>平均數。
  P.s) 由上面兩條可見，平均數很容易受偏差值影響，進而會較靠近偏差之處。

離散趨勢指標：單獨使用集中趨勢指標，難以區辨具有相同集中趨勢指標之資料，儘管實際上他們很不相同。

• 離散趨勢指標，可粗分為兩大類：
• 與範圍(range statistics)有關：
• 全距(range)
• 優點：
1. 容易計算。
2. 易受極端值影響。
3. 可用於順序、等距、比例資料。
• 缺點：
1. 若有界外值存在，容易誤導離散情況。
2. sample size大，其range也大。
3. 沒有使用所有的資料(只使用最大最小值)。
4. 不能用來作統計推論(因容易受極端值影響，並且只使用最大最小值)。
5. 不是用於open-ended categories 以及undeterminalbe scores。
• 四分位距(interquartile range,IQR)：分別將資料切成四等分(25%,50%,75%)，其中50%即為中數(Mdn)。
• 優點：
1. 唯一不受極端值影響的指標(其他都受影響，因其納入平均值)。
2. 唯一可用於open-ended categories和undeterminable scores之離散趨勢指標。
3. 可用於序列、等距與比例資料。
• 缺點：
1. 丟棄太多資料(省略太多資料)。
2. 半四分衛差為(Q3-Q1)/2，有25%之資料量。
• 與集中趨勢指標相關(center-based)：需先知道集中趨勢，方能計算。
• 平均差(似是而非)：將各點與平均數之距離進行平均計算，其結果必然為零，因其正負抵銷之結果。
• 平均絕對差：帶入距離之觀念，使用絕對值表達之。
• 特質：
• 容易了解。
• 使用了所有資料。
• 不可用於open-ended categories and undeterminable scores(因平均數無法處理此狀態，且此項目與平均數相關，因而連帶無法處理)。
• 運算中有絕對值，過程複雜，不受青睞。
• 相較於標準差(standard deviation)，對極端值較不敏感(因SD經過平方與根號處理，仍放大了其差異?)。
• 平均絕對差與中數絕對差：
• 平均絕對差：與平均數比較，取絕對值並加總平均而來。
• 中數絕對差：與中數比較，取絕對值並取中數而來(中數的中數)。
• 變異數：
• 標準差：

Summary：

• 描述統計：以表、圖、數值的方式，解釋統計之結果。
• 表：常見表如次數分配表。
• 圖：常見如長條圖、折線圖、圓餅圖、莖葉圖。
• 偏態：1/N*Sum of (x-u/s)^3
• 峰度：1/N*Sum of (x-u/s)^4-3
• 數值：集中趨勢指標與離散趨勢指標。
• 集中區是指標：Mo、Mdn、Mean。
• 離散趨勢指標： * 自由度(df)
• Range
• range 
• IQR
• Center-based
• average deviation (wrong one)==0
• MAD/Mdn AD
• Variance
• SD
• CV (SD為mean的%)
• 相對地位指標： PR& Z score
• PR< = > 百分位數(反複雜公式)
• 直接看
• 簡單公式：100-(100R-50)/N
• 複雜公式：100/N*(F+x-L/h*f)
• Z score：與標準差比較
• 
  
• 推論統計：
• 好的估計特質：
• 不偏：樣本期望值等同母群體參數者，稱不偏。如樣本變異數是母體變異數的不偏估計。
• 一致：抽取N個樣本時，當N增加可使估計值趨近母體參數者，稱一致。
• 相對有效：比較抽樣分配之標準差(實質為標準誤)，標準誤越小者相對有效越高。
• 充分：是否使用所有資訊。
• 抗拒：是否抵抗極端值。
• 常態分配：
• 特質：
1. 以u為中心對稱。
2. 反曲位於1SD處。
3. 兩端趨近無限大。
4. 曲線下面積為1。
5. 68%資料位於1SD內，95%資料位於2SD內。
6. 偏態系數0，峰度係數3。
• Z分配：
• 常態線性轉換。
• 有參考表可查閱。
• 為常態分布，Z~N(0,1)。
• 抽樣分配：自母群抽取n個樣本無限多次(期望值作法)，將其個別估計值之分配狀態，其標準差以標準誤描述。
• 中央極限定理：自一平均值為u、變異數為s^2之母群，抽取樣本數n，當n變大時使抽樣分配呈現常態分佈，此分布之平均值為u，且其變異數為s^2/n。

Q&A：擬討論問題

1. 平均絕對差與標準差之概念，前者為使用絕對值表現之，因而有正負號的變換問題，而後者使用平方再根號之方式處理，然課程中提及：「平均絕對差對極端值不敏感，但標準差經過平方與根號處理，仍放其差異」，關於此放大之描述為何？ 其如何影響差異？