2013.10.11 心理及教育統計(四)

心理及教育統計 (四)

Review：

• 描述統計：
• 表
• 圖
• 數值：
• 集中趨勢指標(Mo,Mdn,Mean)
• 離散趨勢指標(range & center-based)
• range：全距、四分位距。
• center-based：平均絕對差、變異數...etc。
• 相對地位指標(PR&standard score)：於團體中，個體相對排列位置所在。
• 百分等級：較適合應用到ordinal var.，方法有三：一、直觀排列算比例。二、使用公式，以平均中間概念得。三、使用公式，適用於族群中。
• 百分位數：與百分等級相關，可換算為實際分數(score)，比較其差異，百分等級是以分數歸納其百分等級，而百分位數則是應考多少分數可落於此等第中。
• 標準分數：Z-score/T-score。
• Z-score：原始分數與其平均數相差多少個標準差，屬於沒有單位的數值。可用於不同量尺或者不同測驗之成果。
• Z的平均數必為0，其變異數與標準差必為1。
• 屬於一種線性轉換。
• 可跨組織比對、換算，仍使用分數轉換概念。
• 百分等級vs標準分數：
• PR可用於ordinal data，可知道個體於族群中的相對位置且易於理解，但不知道其實際分數與相較於他人的分數相差多少。
• Z分數可精細描述，不易理解但有科學性，可精細比對不同量尺之資訊，屬於一種線性轉段且不會改變資料間的特質(平移、縮放，但不變形)。然Z分數取得後不會呈現常態分布。
• 線性轉換：影響總表，簡言之可分為平移、縮放，並注意次方關係。
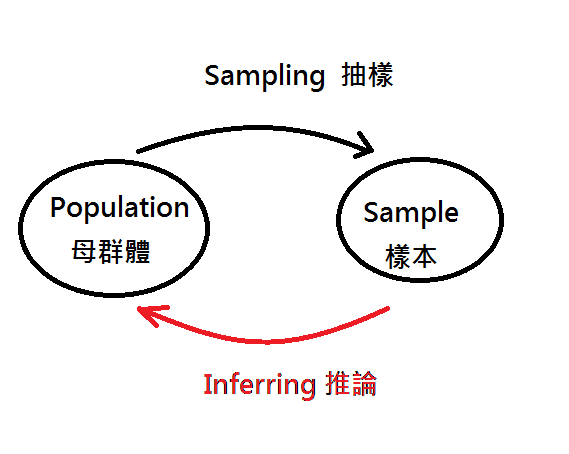
  note：偏態與峰度的計算方式，分別為z的三次與四次方，而如承認線性轉換對Z並不影響，則其對偏態和峰度亦無影響。
• 母群與樣本：
  
• 母群體：希臘符號，變數以參數(parameter)稱之。
• 樣本：英文符號，變數以估計值(estimate)稱之。

Today：

• 一個好的估計值的特質：代表其可充分反應母群體的參數(不知母群參數為前提方須推論)。
• 不偏性(unbiasedness)：當樣本估計期望值等同於母群體參數時，此狀態稱為不偏。
• E(θ-hat)=θ，是不偏估計值，其中θ-hat是估計值，θ是母數。
• E()期望值(expectation)；將無限多個估計值平均起來的值(long-run average)。
• 換言之，經過多次估計平均後，如接近則稱為不偏估計。(p.s 此指多次執行抽樣動作，而非樣本大小)
• 以估計值推測參數平均值時，不偏估計之限制與對應分布型態： ＊此為樣本估計值-->母群體平均值時之關聯性...
• 平均數(mean)，可用於所有分布型態。
• 中數(Mdn)，可用於對稱分配型態。
• 眾數(Mo)，可用於對稱且單峰型態。
  ＊從上列條件中可知，以樣本平均值是最適合用以推估母群體平均值的估計值(廢話)。
• 以估計值歸測參數變異數(標準差)時，樣本變異數是母群變異數的不偏估計：E(s²)=σ²；換言之，E(S²)<σ²。
  note：推論統計討論樣本與母群體之關聯性，變異數(標準差)和平均數之官有密切關係，此部分於後續持續觀察之。
• 相對有效度(relative efficiency)：當兩筆資料都符合一致性的時候，用以比較兩筆資料之優劣。
• 抽樣分配(sampling distribution)：從母群中重複無限多次抽取n個個體(需放回母群，對比抽出後不放回，不造成母群體之改變)，得到的估計值之分配狀態。eg樣本變異數抽樣分配、樣本平均數抽樣分配、樣本XX的抽樣分配(依統計量而定)。
  P.s) 樣本平均數較對稱，而樣本變異數常有偏態。
• 比較估計值抽樣分配的標準差，標準差越小則相對有效度較大。
  note：平均數較中數有效，平均數是一個相對較好的集中趨勢指標。
• 不偏vs有效：<比較之前提為兩者不偏，比較收斂方有意義..>
• 如果E()之後較靠近真實母群數值，則為不偏。
• 如果其分部狀態較集中，則為有效。
• 一致性(consistency)：當樣本數增加 (n↑)時，其估計值相似於母群數值，稱為一致性。
• 平均數有一致性，因平均數使用所有數據，因此當樣本數增加的時候，期望值之精準程度也提升。
• 「不偏不代表一致，一致不代表不偏」：此兩者沒有直接關聯：
• 不偏的概念，是樣本估計值之期望值等於母群體參數。
• 一致的概念，是當樣本數量提升的時候，其變異數(標準差)將隨之縮小的情況。
• 綜論，前者為初始狀態與目標之接近程度，後者為當樣本數增加的時候，其差異會隨之減小的特性。
• 充分性(sufficiency)：是否使用所有數值，如平均數、標準差、變異數皆有，如中數、眾數、四分位數等則無。
• 抗拒性(resistence)：是否能抗拒極端值之影響，如抗拒性大則受影響較小。如眾數、中數、四分位距的抗拒向大(不使用所有數據者往往受影響較小)。
• 常態分配(Normal distribution)：又稱為高斯分配。
• 連續隨機變數的機率分配：將機率的概念引入抽樣中，如於5個球中(3紅2白)抽到白球的機率為2/5，同理將抽樣視為機率，即為於樣本族群中，抽到特定條件者之機率(或與信賴區間有關？ )。
• 機率密度函數(probability density function, pdf)：設x為連續隨機變數，其值介於a,b之間，若f(x)為X的機率密度函數，其滿足：f(x)≧0。
• 累進機率函數
• 期望值
• 變異數
• 標準差
• 常態分配之寫法為X~N(μ,σ²)，由此可知構成條件有二，分別是平均值與標準差。
• 常態分配特性：(68-95-99.7%)
• 以μ為中心之單峰對稱分配。
• 反曲點位於μ±σ。
• 兩尾端無限延伸。
• 常態分配曲線下面積總和為1。
• 於μ±σ(一個標準差間)，其資料量約為68%；μ±2σ間的資料量約為95%。
• 偏態係數為0，峰度係數為3(公式比較會-3校正標準為0)，為一常態峰。
• 常態分配的加法定理：掌握要點為線性轉換對於平均值、標準差之影響，即可詮釋之。
• 定理一：設X~N(μ,σ²)，若W=a+bX，則W~N(a+bμ,b²σ²)。
• 定理二：設X~N(a,b²)、Y~N(c,d²)，若W=eX+fY，則W~N(ea+fc,e²b²⁺f²d²)。
• 標準常態分配(Z分配,standard normal distribution, Z distribution)：滿足條件之分配方式皆可為常態分配，因而可以交織出無限多種平均值與標準差組合，然基於計算方便，將常態分配經線性準換為標準常態分配後，可使用查表之方式迅速獲得結果。
• 利用常態分配加法定理，將Z=(X-μ)/σ，E(Z)=0且Var(Z)=1帶入常態分配機率函數，可得標準常態分配的機率密度函數，Z~N(0,1)。
• 轉換為標準常態分配之好處，可免去個別常態分佈積分之過程，改以查表方式達成計算目標。
  note：±1.96σ，約為兩個標準差的範圍，其內在範圍佔有95%的資料量。
  note2：資料處理的過程中，可從Z推算μ至Z之面積，也可反過來以需要之面積，推算 Z的數值。
  note3：1.645(90%)、1.96(95%)、2.58(99%)是常用的數值。
• 常態分配中的百分等級(percentile,%)：機率有其對應之Z。
• note；考試到本單元結束。