標籤

IRB課程筆記區

問題記錄區：

問題1：計算過程中的標準差、誤差太多，不易區分誰是誰。

紀錄1：
測量標準誤(Standard error of measure) & reliability

參考下圖：


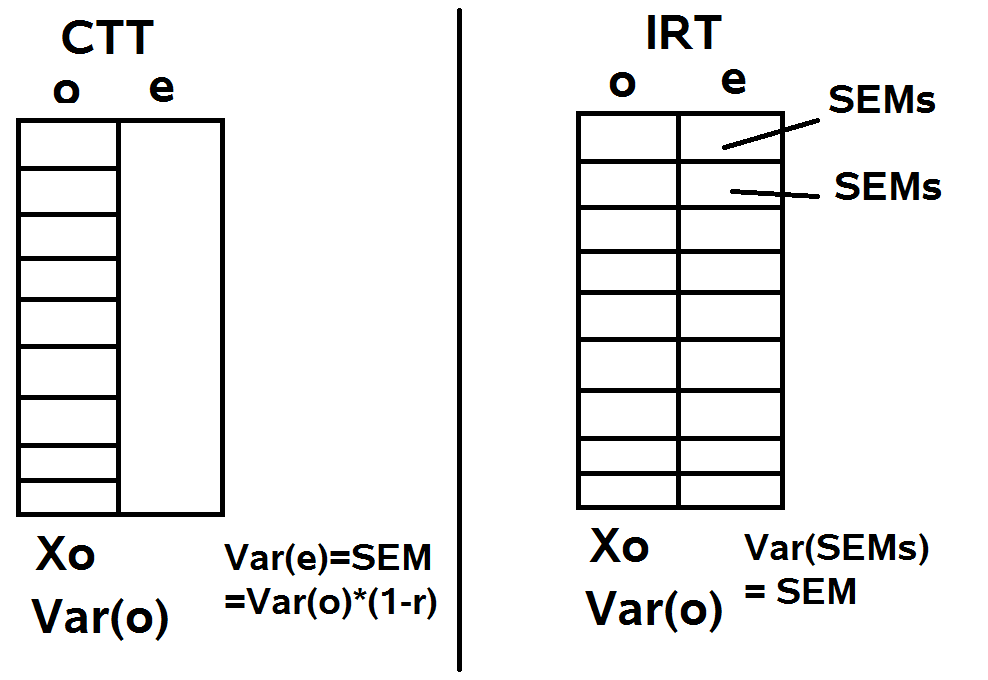
  • 估計標準誤(Standard error of estimate)：以樣本估計能力時的誤差(?)。相當於上圖中的Xo，為所有measures的變異數。
  • 測量標準誤(Standard error of measurement)：以測驗評估個體之能力時的測量誤差。在CTT中假設測驗樣本族群的測量標準誤均(?)一致(為上圖左之SEM)；但在IRT中因可計算不同能力層級的估計誤差，因而可有個體層級的測量標準誤(為上圖中的SEMs)。

==> 名詞附原文，區分來源與概念

補充資料：常見的四種誤差(Error)
1.標準誤(standard error)：指在母群中進行無限多次抽樣，每次抽取n個樣本，並且統計其平均數及變異數，則可得到一抽樣分配資訊。將每一次抽樣結果之變異數進行平均處理，則可得到標準誤。其計算公式為： Ox=O/根號n(其中O代表標準差)。
2.估計標準誤(standard error of estimate)：以一筆資料進行預測時，假使進行無限多次的預測，則每次預測結果均存在一組誤差。將所有誤差加總平均後所得的總變異，稱為估計標準誤。其計算公式為：Syx=Sy*根號1-r^2。
3.測量標準誤(standard error of measure)：以副本方式重複測量一個個案，理論上可得其真實分數。每次測量時可得一組誤差。將所有誤差平均後所得的總誤差，稱為測量標準誤。其計算公式為：SEM=Sx*根號1-r。

問題2：選擇RSM或PCM分析時，可使用Chi-Square Test檢定。其卡方值及自由度如何取得？

紀錄2：計算時的卡方值可從winsteps之table 3.1 取得；自由度的計算概念如下：
  • 假定題目共10題，每題有4個計分類別(表示其有3個steps)
    Free
    Fixed


    Overall
    step

     df
    RSM
    10
    3
    1*1=1
    10+3-1=12
    PCM
    10
    3*10=30
    10*1=10
    10+30-10=30

    30-12=18
    note:
    階難度數量=計分類別數-1
    RSM假定所有題目的階難度差均相同，故只固定一個數值用以估計(固定1)
    PCM假定所有題目均有各自的階難度，故每個題目均需一個數值用以估計(固定數=題數)。
    自由度：自由估計的參數量(扣除固定值)
    如RSM：估計10個題目難度+3個階難度-1=10+3-1=12
    如PCM：估計10個題目難度+每題各3個階難度共30個-每題消耗一個參數共10個=10+10*3-10=30
問題3：為什麼最大概似估計法(MLE)的計算過程中，f(x)定應為ln L一次微分之結果，而不是直接定義f(x)=ln L呢？ 又其中二次微分的意義分別為何？

紀錄3：
  • MLE的概念來自求取最大概率者，而數學上求取極值之方法為取一次微分為零者(代表其斜率為零之轉折處，恰為極值)。但實際上L為連乘，除不易計算之外，數值容易過小也造成操作上的不便，因此，將L取自然對數後的ln L，有計算上之便利。且令ln L最大的x值也會令L最大，因此，可藉由求取ln L的最大值，以完成估計。
  • 而Newton-Raphson的方法，藉由一次微分的方式不斷逼近，以求更精準的估計。 又差異值剛好洽需使用二次微分之函數(詳見補充)。因此，取得一次和二次微分是必須歷經的過程。
  • 實際上，定義f(x)=ln L並非絕對，僅為方便紀錄、表示而已。
    如定義g(x)=ln L，則g'(x)=d ln L/dx，g''(x)=d^ ln L/d^ x。
    又定義f(x)=d ln L，則f'(x)=d^ ln L/d^ x。
問題4：一堆的RSM,PCM又EAP等等，容易混淆。

紀錄4：以下整理這些名詞及概念。
  • Model：
    • 二分計分
      • 單參數模型(1-PL, eg. Rasch)
      • 二參數模型(2-PL)
      • 三參數模型(3-PL)
    • 多分計分
      • Rating Scale Model (RSM) 假定所有階難度均相等(計分類別數也相同)
      • Partial Credit Model (PCM) 假定各題目均有自己的階難度(自由估計之)
      • Generalized Partial Credit Model (GPCM) 為PCM的延伸版，除單純的題目難度與個體能力外，另加入鑑別度的參數。
      • Graded Response Model (GRM) 為累積之機率，分別以不同分數作為切分點，計算其概率。此也可產生類似階難度之數值，然其稱為threshold，特指機率為0.5的能力估計值。
        • 其也可手動轉換圖形為ICC，但須逐步將圖形拆解而來。
        • 在此狀況下，勢必不會出現disordering的狀況。
  • Estimate
    • 能力估計
      • 最大概似估計(MLE)：最直接，但相對繁瑣。且不利於尚未完成之收案，需了解所有反應之後方能計算(又無法用於極端作答狀況)
      • MAP：考慮prior之數值，取posterior的最大概率。
      • EAP：考慮prior之數值，取posterior的期望值。
        • 上述二者均建立在貝氏之條件機率下。然而，如果先天輸入的prior不符合樣本，則會造成明顯的偏差。
問題5：item model fit & principal component analysis (PCA)的差別？
紀錄5：即便符合PCA，如仍有題目misfit，仍須回歸是否刪題之考量，也難以解釋造成此狀況造成之原因。故建議作法為：優先檢驗item model fit，並進行必要的調整，以確認所有題目均落入可接受範圍；再做整理的PCA，使用更多資訊以確保試題符合單向度。

問題6：逐一刪題與一次刪題的差別在於？
紀錄6：刪除題目將造成infit & outfit之MNSQ的些許變動，可能造成原位於邊界的題目超過(或者符合)標準，進而影響題目之判讀。另，如果一次刪除所有題目，可能造成一些題目被誤刪之狀況(即逐一刪除可保留，但一次刪除就全數刪去之狀況)，可能造成題目數量過少以影響信度之問題。建議之作法為逐一刪除，並優先挑選最misfit之題目進行刪除，可較謹慎的處理此問題。 另，也可比較刪除之後之能力估計是否呈現顯著差異；或已知某些題目misfit，可優先估計其他題目，等確立之後，再固定這些題目的難度重新估計這些疑似有問題的題目之難度(參考二次估計之紀錄)

-----------------------------------------------------------------------------------------------------------
軟體操作備忘區：

Winsteps操作紀錄：
  • Winsteps軟體操作包含三個E(enter)之主要程序：
    1. 開啟指令
    2. 設定輸出名稱
    3. 是否有其它調整(通常無)
  • 指令撰寫格式&常用指令
    • 必寫內容：
      ; This is the control file     <=名稱
      &INST                           <=正式指令宣告
      TITLE='apple'                <=標題叫做apple
      (DATA=apples.txt)        <=如資料不與本指令檔合併，則須輸入
      NI=30                            <=題目數量為30題
      CODES=0123               <=最大計分類別數
      (group=0)                       <=若不寫入則為RSM；若寫入並=0則為PCM
      NAME1=0                     <=姓名標籤之起始行數
      ITEM1=20                     <=作答反應之起始行數
      TFILE=*                        <=輸出表單代碼。分析完成之後亦可手動點選所需資料。
      1.2
      3.1
      6.1
      10.1
      *
      &END                            <=宣告指令輸入結束
      (ITEM1                          <=指定項目名稱
      ITEM2
      ITEM3...)
      END NAMES                <=宣告名稱輸入結束
      (data)                              <=可放資料(或使用data=apple.txt取代)
    • 常用指令：
      • IDFILE=**           <=用以刪除特定題目
      • PRCOMP=S         <=帶入PCA分析   


標籤：

留言

張貼留言

熱門文章